来自：查字典高考网 2017-01-21
对于高中生而言，要用常规方法求解某些函数的最值，是非常困难的，甚至不知道如何下手，但是善于利用函数的几何意义，把所给函数整理变形，便立即可以看出明确的几何意义，从而利用变形后函数所呈现出的几何意义，数形结合，进行求解函数的最值问题。
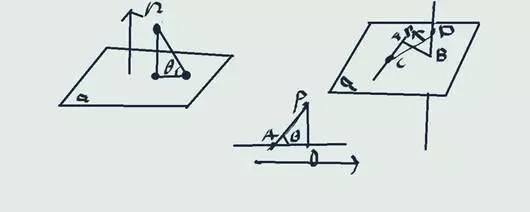
首先我们先来看看点到直线的距离，已知一点P(x0,y0)以及直线方程Ax+By+C=0，求点到直线的距离公式，如下图所示：
下面我们具体看一个例题，看看如何利用点到直线的距离的几何意义，求解函数的最值问题的。
例题：求下图1所示函数的最大值、最小值，题目如下图所示：
接下来我们对原函数进行变形处理，具体变形步骤如下图所示，首先需要对函数进行适当的变形，使变形后的函数满足点到直线的距离公式，这个过程就是点到直线距离公式的配凑过程。
然后我们对点(x,(4-(x-2)^2)^(1/2))作分析，把它变成参数方程，则有x0=t,y0=(4-(t-2)^2)^(1/2)。因为(x0-2)^2+y0^2=(t-2)^2+4-(t-2)^2=4，显然x0,y0满足以(2,0)点为圆心，半径为2的圆，且是上半圆，因为y00的。
我们画出直线方程和满足x0,y0的原方程图像，具体图像如下图所示，非常简单，直线方程时一条直线，还有一个以(2,0)点为圆心，半径为2的圆的上半圆。
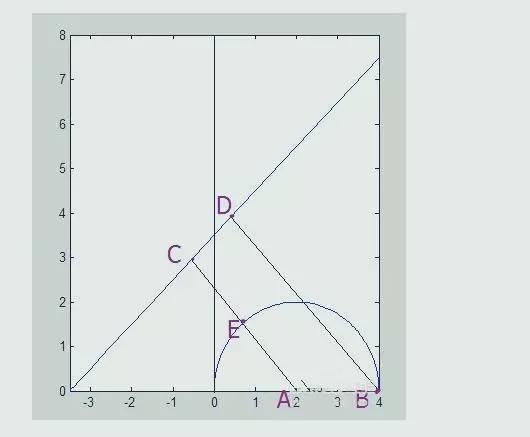
画出图形后，数形结合，在图上过圆心A作直线的垂线，交直线于C点，交圆于E点，在过圆最右端点B作直线的垂线，交直线于D,则很明显圆上点到直线的最小距离是CE,最大距离是BD，再次利用点距离距离公式，计算出CE、BD的大小，即可求得原函数的最值。计算过程如下图所示：
上面我们求出了圆上点到直线的最大最小值，分别为BD、CE长度，将这两个值代入原函数的变形表达式中，可得到函数的最大、最小值。具体如下所示：
注意：关键在于函数如何变形为点到直线距离公式的形式。
【巧用点到直线距离的几何意义求函数最值！】相关文章：
★ 情绪与心理健康
一边扔试卷一边玩摇滚？这个学校的高考减压方式，真是帅到没朋友
创艺第二届：2019届高考录取表彰大会暨“核桃音乐节”合影——你只管努力，剩下的交给创艺
加油吧考生：2019高考咨询大直播 第43集 科学填报志愿 规划精彩人生
学渣儿子高考，英语选择题全选B！老师通报成绩的那一刻父亲懵了
探秘历史 第二季 第233集 考英语用来睡觉，结果仍是高考状元，如今她怎么样了？
张雪峰高考志愿填报指南 第47集 高考志愿，令人头疼的数学系，才是专业万金油，毕业后机会多
乾坤已定，组合解读2019高考数学全国3卷理科18题，你是黑马吗？
沈阳音乐学院郎亦农教授的女高音高考曲目解析课程 第1集 沈阳音乐学院郎亦农为你讲解女高音高考曲目
葛军大爷怒了：高考我出了个小学数学送分题，你们跟我说不会做？
张雪峰高考志愿填报指南 第15集 高考填报志愿，想学电子信息类专业，推荐报这六所高校，不出错
