来自:查字典高考网 2017-01-21
对于高中生而言,要用常规方法求解某些函数的最值,是非常困难的,甚至不知道如何下手,但是善于利用函数的几何意义,把所给函数整理变形,便立即可以看出明确的几何意义,从而利用变形后函数所呈现出的几何意义,数形结合,进行求解函数的最值问题。
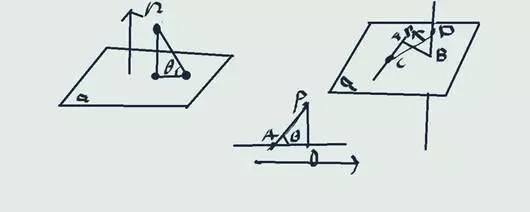
首先我们先来看看点到直线的距离,已知一点P(x0,y0)以及直线方程Ax+By+C=0,求点到直线的距离公式,如下图所示:

下面我们具体看一个例题,看看如何利用点到直线的距离的几何意义,求解函数的最值问题的。
例题:求下图1所示函数的最大值、最小值,题目如下图所示:

接下来我们对原函数进行变形处理,具体变形步骤如下图所示,首先需要对函数进行适当的变形,使变形后的函数满足点到直线的距离公式,这个过程就是点到直线距离公式的配凑过程。

然后我们对点(x,(4-(x-2)^2)^(1/2))作分析,把它变成参数方程,则有x0=t,y0=(4-(t-2)^2)^(1/2)。因为(x0-2)^2+y0^2=(t-2)^2+4-(t-2)^2=4,显然x0,y0满足以(2,0)点为圆心,半径为2的圆,且是上半圆,因为y00的。
我们画出直线方程和满足x0,y0的原方程图像,具体图像如下图所示,非常简单,直线方程时一条直线,还有一个以(2,0)点为圆心,半径为2的圆的上半圆。
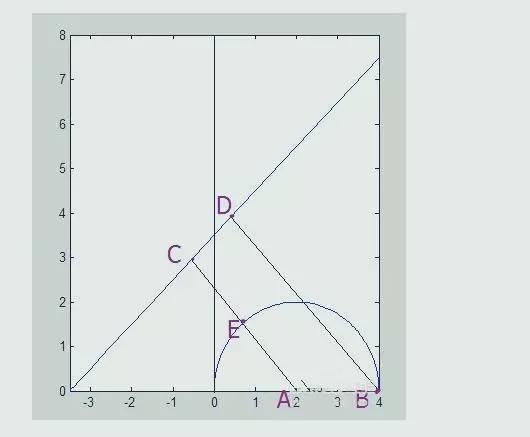
画出图形后,数形结合,在图上过圆心A作直线的垂线,交直线于C点,交圆于E点,在过圆最右端点B作直线的垂线,交直线于D,则很明显圆上点到直线的最小距离是CE,最大距离是BD,再次利用点距离距离公式,计算出CE、BD的大小,即可求得原函数的最值。计算过程如下图所示:

上面我们求出了圆上点到直线的最大最小值,分别为BD、CE长度,将这两个值代入原函数的变形表达式中,可得到函数的最大、最小值。具体如下所示:

注意:关键在于函数如何变形为点到直线距离公式的形式。
【巧用点到直线距离的几何意义求函数最值!】相关文章:
沈阳音乐学院郎亦农教授的女高音高考曲目解析课程 第9集 《赛吾里麦》演唱讲解,音乐表现一定要自然流畅
1000张学生用草稿纸考研专用免邮空白便宜薄演草演算纸白纸本书写纸批发打草a4大张实惠装18k高考数学草稿本
探秘历史 第二季 第479集 河南叛逆高考生,写下8000字批判作文,现状如何?
视频|2019全国高考今日开考: 语文特级教师评析上海卷高考作文
高考阅卷名师给考生的高考作文密训课 第3集 高考作文审题实操方法精讲(一)
一边扔试卷一边玩摇滚?这个学校的高考减压方式,真是帅到没朋友
衍声高考琴行2019高本硕学生暑假音乐会 张俊瀚《陕北民歌主题变奏曲》《阿根廷舞曲》第三乐章
沈阳音乐学院郎亦农教授的女高音高考曲目解析课程 第1集 沈阳音乐学院郎亦农为你讲解女高音高考曲目