来自：查字典高考网 2009-08-31
【竞赛知识点拨】
1． 线段或角相等的证明
（1） 利用全等△或相似多边形；
（2） 利用等腰△；
（3） 利用平行四边形；
（4） 利用等量代换；
（5） 利用平行线的性质或利用比例关系
（6） 利用圆中的等量关系等。
2． 线段或角的和差倍分的证明
（1） 转化为相等问题。如要证明a=bc，可以先作出线段p=bc，再去证明a=p，即所谓截长补短，角的问题仿此进行。
（2） 直接用已知的定理。例如：中位线定理，Rt△斜边上的中线等于斜边的一半；△的外角等于不相邻的内角之和；圆周角等于同弧所对圆心角的一半等等。
3． 两线平行与垂直的证明
（1） 利用两线平行与垂直的判定定理。
（2） 利用平行四边形的性质可证明平行；利用等腰△的三线合一可证明垂直。
（3） 利用比例关系可证明平行；利用勾股定理的逆定理可证明垂直等。
【竞赛例题剖析】
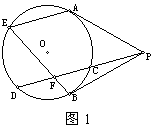
【例1】从⊙O外一点P向圆引两条切线PA、PB和割线PCD。从A点作弦AE平行于CD，连结BE交CD于F。求证：BE平分CD。
【分析1】构造两个全等△。
连结ED、AC、AF。
CF=DF△ACF≌△EDF
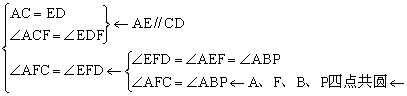
PAB=AEB=PFB
【分析2】利用圆中的等量关系。连结OF、OP、OB。
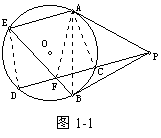
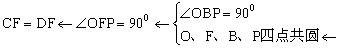
PFB=POB
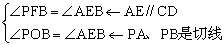
注：连结OP、OA、OF，证明A、O、F、P四点共圆亦可。
【例2】
△ABC内接于⊙O，P是弧 AB上的一点，过P作OA、OB的垂线，与AC、BC分别交于S、T，AB交于M、N。求证：PM=MS充要条件是PN=NT。
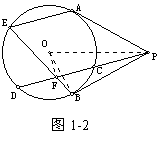
【分析】只需证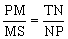
， PMPN=MSNT。
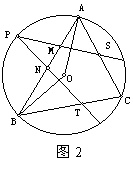（2，4）△APM∽△PBN
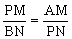PMPN=AMBN
（BNT=AMS，BTN=MAS）△BNT∽△SMA
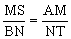MSNT=AMBN
【例3】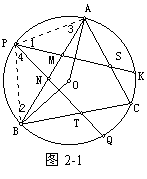
已知A为平面上两半径不等的圆O1和O2的一个交点，两外公切线P1P2、Q1Q2分别切两圆于P1、P2、Q1、Q2，M1、M2分别为P1Q1、P2Q2的中点。求证：O1AO2=M1AM2。
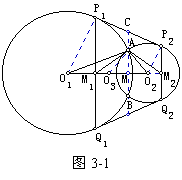
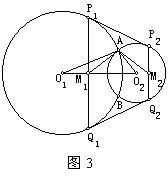
【分析】设B为两圆的另一交点，连结并延长BA交P1P2于C，交O1O2于M，则C为P1P2的中点，且P1M1∥CM∥P2M2，故CM为M1M2的中垂线。
在O1M上截取MO3=MO2，则M1AO3=M2AO2。
故只需证O1AM1=O3AM1，即证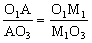
。
由△P1O1M1∽P2O2M2，M1O3=M2O2，O1P1=O1A，O2P2=O2A可得。
【例4】在△ABC中，ABAC，A的外角平分线交△ABC的外接圆于D，DEAB于E，求证：AE=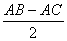
。
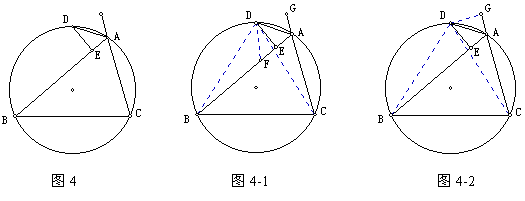【分析】方法1、2AE=AB-AC
在BE上截取EF=AE，只需证BF=AC，连结DC、DB、DF，从而只需证△DBF≌△DCA
DF=DA，DBF=DCA，DFB=DAC
DFA=DAF=DAG。
方法2、延长CA至G，使AG=AE，则只需证BE=CG
连结DG、DC、DB，则只需证△DBE≌△DCG
DE=DG，DBE=DCG，DEB=DGC=Rt。
【例5】ABC的顶点B在⊙O外，BA、BC均与⊙O相交，过BA与圆的交点K引ABC平分线的垂线，交⊙O于P，交BC于M。
求证：线段PM为圆心到ABC平分线距离的2倍。
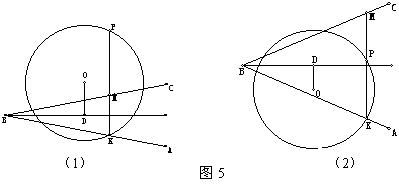【分析】若角平分线过O，则P、M重合，PM=0，结论显然成立。
若角平分线不过O，则延长DO至D，使OD=OD，则只需证DD=PM。连结DP、DM，则只需证DMPD为平行四边形。
过O作mPK，则D
D,K
P，DPK=DKP
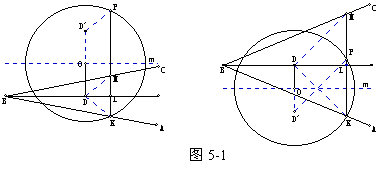BL平分ABC，MKBLBL为MK的中垂线DKB=DMK
DPK=DMK，DP∥DM。而D D∥PM，
DMPD为平行四边形。
【例6】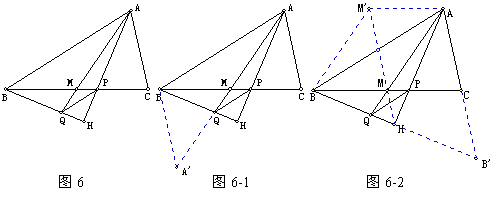
在△ABC中，AP为A的平分线，AM为BC边上的中线，过B作BHAP于H，AM的延长线交BH于Q，求证：PQ∥AB。
【分析】方法1、结合中线和角平分线的性质，考虑用比例证明平行。
倍长中线：延长AM至M，使AM=MA，连结BA，如图6-1。
PQ∥AB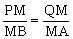
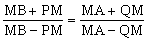
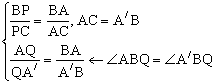
ABQ=180HBA+BAH+CAP)= 180-90CAP=90BAP=ABQ
方法2、结合角平分线和BHAH联想对称知识。
延长BH交AC的延长线于B，如图6-2。则H为BB的中点，因为M为BC的中点，连结HM，则HM∥B/C。延长HM交AB于O，则O为AB的中点。延长MO至M，使OM=OM，连结MA、MB，则AMBM是平行四边形，
MP∥AM，QM∥BM。于是，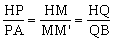
，所以PQ∥AB。
【例7】
菱形ABCD的内切圆O与各边分别切于E、F、G、H，在EF与GH上分别作⊙O的切线交AB于M，交BC于N，交CD于P，交DA于Q。
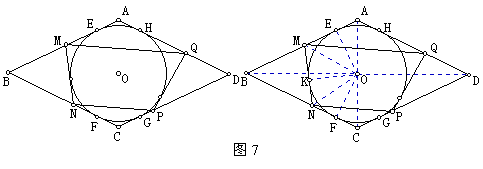求证：MQ∥NP。（95年全国联赛二试3）
【分析】由AB∥CD知：要证MQ∥NP，只需证AMQ=CPN，
结合C知，只需证△AMQ∽△CPN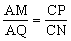
，AMCN=AQCP。
连结AC、BD，其交点为内切圆心O。设MN与⊙O切于K，连结OE、OM、OK、ON、OF。记ABO=，MOK=，KON=，则
EOM=，FON=，EOF=2+2=180。
BON=90NOF-COF=90-=
CNO=NBO+NOB=+=AOE+MOE=AOM
又OCN=MAO，△OCN∽△MAO，于是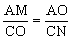
，
AMCN=AOCO
同理，AQCP=AOCO。
【例8】ABCD是圆内接四边形，其对角线交于P，M、N分别是AD、BC的中点，过M、N分别作BD、AC的垂线交于K。求证：KPAB。
【分析】延长KP交AB于L，则只需证PAL+APL=90，
即只需证PDC+KPC=90，只需证PDC=PKF，
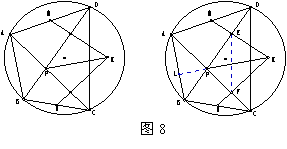因为P、F、K、E四点共圆，故只需证PDC=PEF，即EF∥DC。
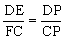
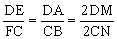
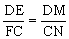△DME∽△CNF
【例9】以△ABC的边BC为直径作半圆，与AB、AC分别交于点D、E。过D、E作BC的垂线，垂足分别是F、G，线段DG、EF交于点M。求证：AMBC。
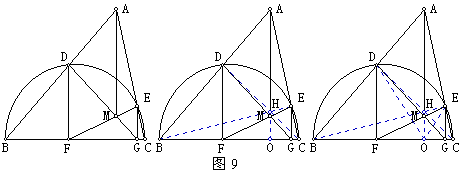
【分析】连结BE、CD交于H，则H为垂心，故AHBC。（同一法）
设AHBC于O，DG、AH交于M1，EF、AH交于M2。下面证M1、M2重合。
OM1∥DF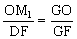
OM1=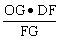
。
OM2∥EG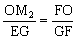
OM2=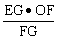
。
只需证OGDF=EGOF，即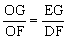
Rt△OEG∽Rt△ODFDOF=DHB=EHC=EOG。
【竞赛专题讲座－平面几何证明】相关文章：
[标签：推理与证明,几何,几何问题,讲座]
四川省宜宾县2016届高三第一次适应性测试语文试题（含答案）
宁夏大学附属中学2016届高三下学期第二次模拟考试语文试题（含答案）
福建省漳州市2016年5月普通高中毕业班质量检查语文试卷（含答案）
河南省洛阳市第一高中2016届高三下学期第二次仿真模拟语文试题（含答案）
江西省2016年高中毕业班新课程教学质量监测语文试题（含答案）
衍声高考琴行2019高本硕学生暑假音乐会 张俊瀚《陕北民歌主题变奏曲》《阿根廷舞曲》第三乐章
探秘历史 第二季 第233集 考英语用来睡觉，结果仍是高考状元，如今她怎么样了？
加油吧考生：2019高考咨询大直播 第43集 科学填报志愿 规划精彩人生
学渣儿子高考，英语选择题全选B！老师通报成绩的那一刻父亲懵了
视频|2019全国高考今日开考: 语文特级教师评析上海卷高考作文
沈阳音乐学院郎亦农教授的女高音高考曲目解析课程 第1集 沈阳音乐学院郎亦农为你讲解女高音高考曲目
张雪峰高考志愿填报指南 第47集 高考志愿，令人头疼的数学系，才是专业万金油，毕业后机会多
张雪峰高考志愿填报指南 第15集 高考填报志愿，想学电子信息类专业，推荐报这六所高校，不出错
amc传媒音乐影像 第一季 第598集 西安原创乐队走进英泰青卓 用音乐助力高考学子
2019全国高考志愿填报攻略 第50集 天津市高考历史三年本科录取排名
他高考作文仅得6分，总分428分，被985高校录取，却被导师拒绝！
