来自：查字典高考网 2009-08-31
【竞赛知识点拨】
1． 线段或角相等的证明
（1） 利用全等△或相似多边形；
（2） 利用等腰△；
（3） 利用平行四边形；
（4） 利用等量代换；
（5） 利用平行线的性质或利用比例关系
（6） 利用圆中的等量关系等。
2． 线段或角的和差倍分的证明
（1） 转化为相等问题。如要证明a=bc，可以先作出线段p=bc，再去证明a=p，即所谓截长补短，角的问题仿此进行。
（2） 直接用已知的定理。例如：中位线定理，Rt△斜边上的中线等于斜边的一半；△的外角等于不相邻的内角之和；圆周角等于同弧所对圆心角的一半等等。
3． 两线平行与垂直的证明
（1） 利用两线平行与垂直的判定定理。
（2） 利用平行四边形的性质可证明平行；利用等腰△的三线合一可证明垂直。
（3） 利用比例关系可证明平行；利用勾股定理的逆定理可证明垂直等。
【竞赛例题剖析】
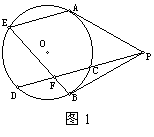
【例1】从⊙O外一点P向圆引两条切线PA、PB和割线PCD。从A点作弦AE平行于CD，连结BE交CD于F。求证：BE平分CD。
【分析1】构造两个全等△。
连结ED、AC、AF。
CF=DF△ACF≌△EDF
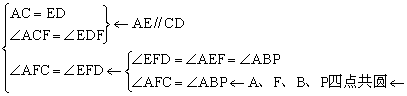
PAB=AEB=PFB
【分析2】利用圆中的等量关系。连结OF、OP、OB。
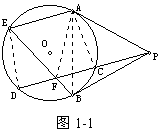
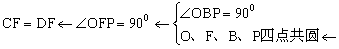
PFB=POB
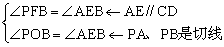
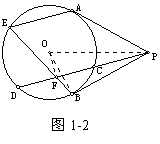注：连结OP、OA、OF，证明A、O、F、P四点共圆亦可。
【例2】
△ABC内接于⊙O，P是弧 AB上的一点，过P作OA、OB的垂线，与AC、BC分别交于S、T，AB交于M、N。求证：PM=MS充要条件是PN=NT。
【分析】只需证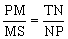
， PMPN=MSNT。
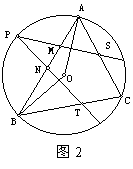（2，4）△APM∽△PBN
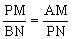PMPN=AMBN
（BNT=AMS，BTN=MAS）△BNT∽△SMA
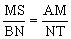MSNT=AMBN
【例3】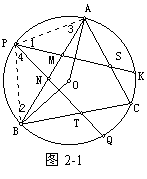
已知A为平面上两半径不等的圆O1和O2的一个交点，两外公切线P1P2、Q1Q2分别切两圆于P1、P2、Q1、Q2，M1、M2分别为P1Q1、P2Q2的中点。求证：O1AO2=M1AM2。
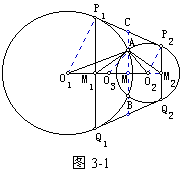
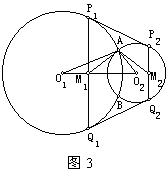
【分析】设B为两圆的另一交点，连结并延长BA交P1P2于C，交O1O2于M，则C为P1P2的中点，且P1M1∥CM∥P2M2，故CM为M1M2的中垂线。
在O1M上截取MO3=MO2，则M1AO3=M2AO2。
故只需证O1AM1=O3AM1，即证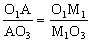
。
由△P1O1M1∽P2O2M2，M1O3=M2O2，O1P1=O1A，O2P2=O2A可得。
【例4】在△ABC中，ABAC，A的外角平分线交△ABC的外接圆于D，DEAB于E，求证：AE=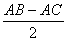
。
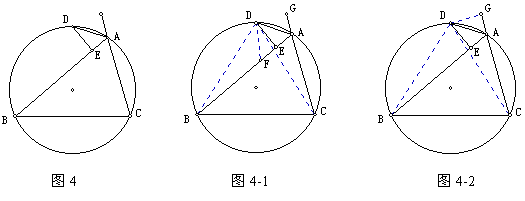【分析】方法1、2AE=AB-AC
在BE上截取EF=AE，只需证BF=AC，连结DC、DB、DF，从而只需证△DBF≌△DCA
DF=DA，DBF=DCA，DFB=DAC
DFA=DAF=DAG。
方法2、延长CA至G，使AG=AE，则只需证BE=CG
连结DG、DC、DB，则只需证△DBE≌△DCG
DE=DG，DBE=DCG，DEB=DGC=Rt。
【例5】ABC的顶点B在⊙O外，BA、BC均与⊙O相交，过BA与圆的交点K引ABC平分线的垂线，交⊙O于P，交BC于M。
求证：线段PM为圆心到ABC平分线距离的2倍。
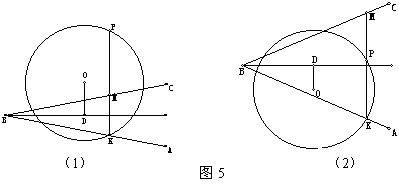【分析】若角平分线过O，则P、M重合，PM=0，结论显然成立。
若角平分线不过O，则延长DO至D，使OD=OD，则只需证DD=PM。连结DP、DM，则只需证DMPD为平行四边形。
过O作mPK，则D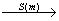
D,K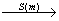
P，DPK=DKP
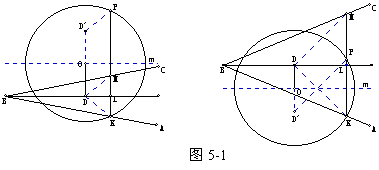BL平分ABC，MKBLBL为MK的中垂线DKB=DMK
DPK=DMK，DP∥DM。而D D∥PM，
DMPD为平行四边形。
【例6】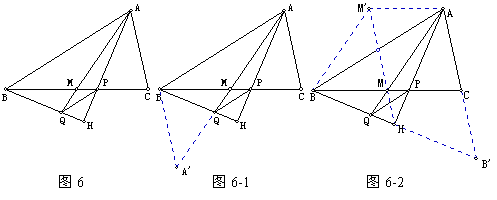
在△ABC中，AP为A的平分线，AM为BC边上的中线，过B作BHAP于H，AM的延长线交BH于Q，求证：PQ∥AB。
【分析】方法1、结合中线和角平分线的性质，考虑用比例证明平行。
倍长中线：延长AM至M，使AM=MA，连结BA，如图6-1。
PQ∥AB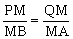
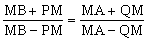
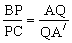
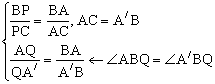
ABQ=180HBA+BAH+CAP)= 180-90CAP=90BAP=ABQ
方法2、结合角平分线和BHAH联想对称知识。
延长BH交AC的延长线于B，如图6-2。则H为BB的中点，因为M为BC的中点，连结HM，则HM∥B/C。延长HM交AB于O，则O为AB的中点。延长MO至M，使OM=OM，连结MA、MB，则AMBM是平行四边形，
MP∥AM，QM∥BM。于是，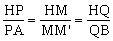
，所以PQ∥AB。
【例7】
菱形ABCD的内切圆O与各边分别切于E、F、G、H，在EF与GH上分别作⊙O的切线交AB于M，交BC于N，交CD于P，交DA于Q。
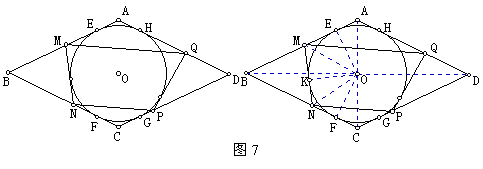求证：MQ∥NP。（95年全国联赛二试3）
【分析】由AB∥CD知：要证MQ∥NP，只需证AMQ=CPN，
结合C知，只需证△AMQ∽△CPN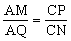
，AMCN=AQCP。
连结AC、BD，其交点为内切圆心O。设MN与⊙O切于K，连结OE、OM、OK、ON、OF。记ABO=，MOK=，KON=，则
EOM=，FON=，EOF=2+2=180。
BON=90NOF-COF=90-=
CNO=NBO+NOB=+=AOE+MOE=AOM
又OCN=MAO，△OCN∽△MAO，于是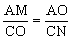
，
AMCN=AOCO
同理，AQCP=AOCO。
【例8】ABCD是圆内接四边形，其对角线交于P，M、N分别是AD、BC的中点，过M、N分别作BD、AC的垂线交于K。求证：KPAB。
【分析】延长KP交AB于L，则只需证PAL+APL=90，
即只需证PDC+KPC=90，只需证PDC=PKF，
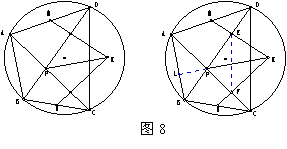因为P、F、K、E四点共圆，故只需证PDC=PEF，即EF∥DC。
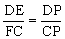
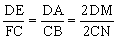
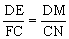△DME∽△CNF
【例9】以△ABC的边BC为直径作半圆，与AB、AC分别交于点D、E。过D、E作BC的垂线，垂足分别是F、G，线段DG、EF交于点M。求证：AMBC。
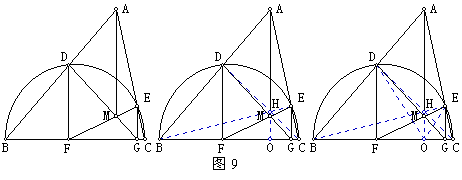
【分析】连结BE、CD交于H，则H为垂心，故AHBC。（同一法）
设AHBC于O，DG、AH交于M1，EF、AH交于M2。下面证M1、M2重合。
OM1∥DF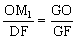
OM1=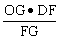
。
OM2∥EG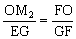
OM2=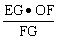
。
只需证OGDF=EGOF，即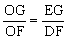
Rt△OEG∽Rt△ODFDOF=DHB=EHC=EOG。
【竞赛专题讲座－平面几何证明】相关文章：
★ 1998中国数学奥林匹克（广州）（第十三届全国中学生数学冬令营）
★ 染色方法
★ 分类与讨论
★ 同余式与不定方程
★ 建模概论
[标签：推理与证明,几何,几何问题,讲座]
竞赛专题讲座－平面几何证明 
竞赛专题讲座－平面几何四个重要定理 竞赛专题讲座－平面几何证明 
覆盖 
平面图形的面积 
抽屉原则 高考阅卷名师给考生的高考作文密训课 第3集 高考作文审题实操方法精讲（一）
高中语文知识清单高考语文总複习工具书第5次修订五全綵版五三曲一线科学备考基础知识手册知识大集结资料书参考书导书高一高二高三
探秘历史 第二季 第211集 此人高考数学考了0分，因作文写3句话被重点大学录取
张雪峰高考志愿填报指南 第15集 高考填报志愿，想学电子信息类专业，推荐报这六所高校，不出错
张雪峰高考志愿填报指南 第28集 高考志愿分析，材料科学与工程专业，就业很一般，建议慎重选择
爆笑班主任 第一季 第220集 高考前最后一只视频，山东王老师揭秘高考的秘密
一边扔试卷一边玩摇滚？这个学校的高考减压方式，真是帅到没朋友
沈阳音乐学院郎亦农教授的女高音高考曲目解析课程 第9集 《赛吾里麦》演唱讲解，音乐表现一定要自然流畅
学渣儿子高考，英语选择题全选B！老师通报成绩的那一刻父亲懵了
高考前必听的5首励志歌曲，《Dream it possible》最能鼓舞人心！
