来自：查字典高考网 2009-08-31
四个重要定理：
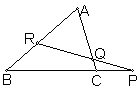梅涅劳斯(Menelaus)定理（梅氏线）
△ABC的三边BC、CA、AB或其延长线上有点P、Q、R，则P、Q、R共线的充要条件是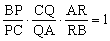 
。
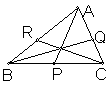塞瓦(Ceva)定理（塞瓦点）
△ABC的三边BC、CA、AB上有点P、Q、R，则AP、BQ、CR共点的充要条件是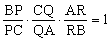
。
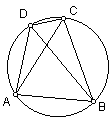
托勒密(Ptolemy)定理
四边形的两对边乘积之和等于其对角线乘积的充要条件是该四边形内接于一圆。
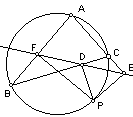
西姆松(Simson)定理（西姆松线）
从一点向三角形的三边所引垂线的垂足共线的充要条件是该点落在三角形的外接圆上。
例题：
1． 
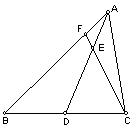设AD是△ABC的边BC上的中线，直线CF交AD于F。求证：
。
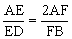【分析】CEF截△ABD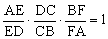
（梅氏定理）
【评注】也可以添加辅助线证明：过A、B、D之一作CF的平行线。
2． 
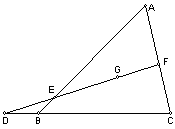过△ABC的重心G的直线分别交AB、AC于E、F，交CB于D。
求证：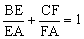
。
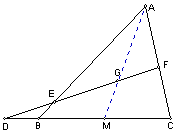【分析】连结并延长AG交BC于M，则M为BC的中点。
DEG截△ABM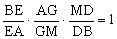
（梅氏定理）
DGF截△ACM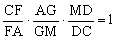
（梅氏定理）
=
=
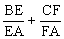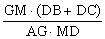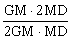=1
【评注】梅氏定理
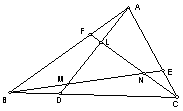
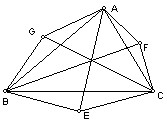
3． D、E、F分别在△ABC的BC、CA、AB边上，
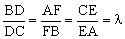，AD、BE、CF交成△LMN。
求S△LMN。
【分析】
【评注】梅氏定理
4． 以△ABC各边为底边向外作相似的等腰△BCE、△CAF、△ABG。求证：AE、BF、CG相交于一点。
【分析】
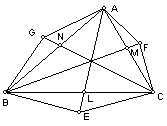
【评注】塞瓦定理
5． 
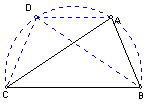已知△ABC中，B=2C。求证：AC2=AB2+ABBC。
【分析】过A作BC的平行线交△ABC的外接圆于D，连结BD。则CD=DA=AB，AC=BD。
由托勒密定理，ACBD=ADBC+CDAB。
【评注】托勒密定理
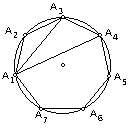
6． 已知正七边形A1A2A3A4A5A6A7。
求证：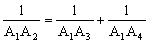
。（第21届全苏数学竞赛）
【分析】
【评注】托勒密定理
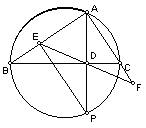
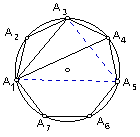
7． △ABC的BC边上的高AD的延长线交外接圆于P，作PEAB于E，延长ED交AC延长线于F。
求证：BCEF=BFCE+BECF。
【分析】
【评注】西姆松定理（西姆松线）
8． 
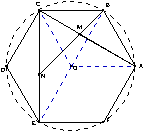正六边形ABCDEF的对角线AC、CE分别被内分点M、N分成的比为AM：AC=CN：CE=k，且B、M、N共线。求k。（23-IMO-5）
【分析】
【评注】面积法
9． 
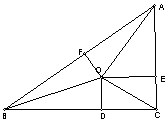O为△ABC内一点，分别以da、db、dc表示O到BC、CA、AB的距离，以Ra、Rb、Rc表示O到A、B、C的距离。
求证：（1）aRabdb+cdc;
(2) aRacdb+bdc;
(3) Ra+Rb+Rc2(da+db+dc)。
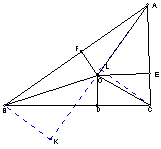【分析】
【评注】面积法
10．△ABC中，H、G、O分别为垂心、重心、外心。
求证：H、G、O三点共线，且HG=2GO。（欧拉线）
【分析】
【评注】同一法
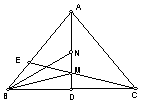
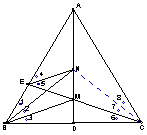
11．△ABC中，AB=AC，ADBC于D，BM、BN三等分ABC，与AD相交于M、N，延长CM交AB于E。
求证：MB//NE。
【分析】
【评注】对称变换
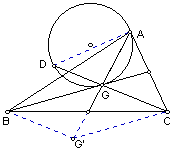
12．
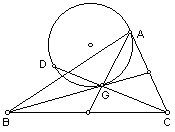G是△ABC的重心，以AG为弦作圆切BG于G，延长CG交圆于D。求证：AG2=GCGD。
【分析】
【评注】平移变换
13．
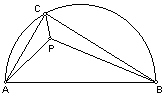C是直径AB=2的⊙O上一点，P在△ABC内，若PA+PB+PC的最小值是
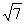，求此时△ABC的面积S。
【分析】
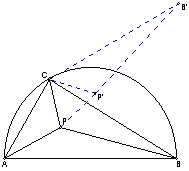
【评注】旋转变换
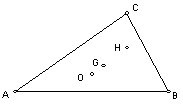
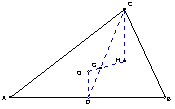
费马点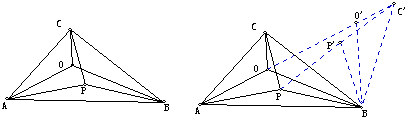
：已知O是△ABC内一点，AOB=BOC=COA=120；P是△ABC内任一点，求证：PA+PB+PCOA+OB+OC。（O为费马点）
【分析】将C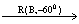
C，O
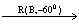O， P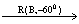
P，连结OO、PP。则△B OO、△B PP都是正三角形。
OO=OB，PP =PB。显然△BOC≌△BOC，△BPC≌△BPC。
由于BOC=BOC=120=180BOO，A、O、O、C四点共线。
AP+PP+PCAC=AO+OO+OC，即PA+PB+PCOA+OB+OC。
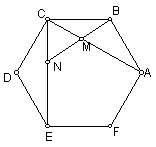
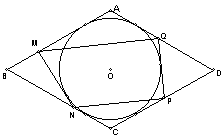14．(95全国竞赛) 菱形ABCD的内切圆O与各边分别交于E、F、G、H，在弧EF和弧GH上分别作⊙O的切线交AB、BC、CD、DA分别于M、N、P、Q。
求证：MQ//NP。
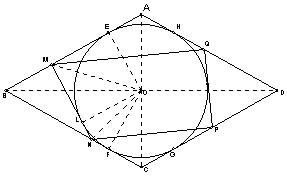【分析】由AB∥CD知：要证MQ∥NP，只需证AMQ=CPN，
结合C知，只需证
△AMQ∽△CPN
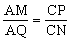，AMCN=AQCP。
连结AC、BD，其交点为内切圆心O。设MN与⊙O切于K，连结OE、OM、OK、ON、OF。记ABO=，MOK=，KON=，则
EOM=，FON=，EOF=2+2=180。
BON=90NOF-COF=90-=
CNO=NBO+NOB=+=AOE+MOE=AOM
又OCN=MAO，△OCN∽△MAO，于是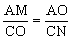
，
AMCN=AOCO
同理，AQCP=AOCO。
【评注】
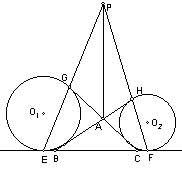
15．(96全国竞赛)⊙O1和⊙O2与ABC的三边所在直线都相切，E、F、G、H为切点，EG、FH的延长线交于P。求证：PABC。
【分析】
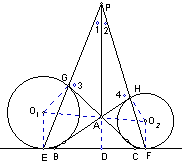
【评注】
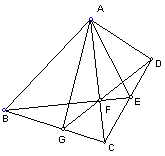
16．(99全国竞赛)如图，在四边形ABCD中，对角线AC平分BAD。在CD上取一点E，BE与AC相交于F，延长DF交BC于G。求证：GAC=EAC。
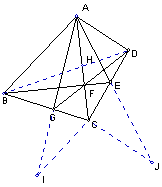证明：连结BD交AC于H。对△BCD用塞瓦定理，可得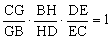
因为AH是BAD的角平分线，由角平分线定理，
可得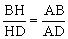
，故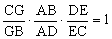
。
过C作AB的平行线交AG的延长线于I，过C作AD的平行线交AE的延长线于J。
则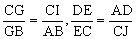
，
所以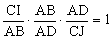
，从而CI=CJ。
又因为CI//AB，CJ//AD，故ACI=BAC=DAC=ACJ。
因此，△ACI≌△ACJ，从而IAC=JAC，即GAC=EAC。
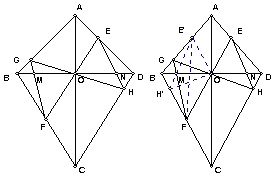已知AB=AD，BC=DC，AC与BD交于O，过O的任意两条直线EF和GH与四边形ABCD的四边交于E、F、G、H。连结GF、EH，分别交BD于M、N。求证：OM=ON。（5届CMO）
证明：作△EOH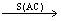
△EOH，则只需证E、M、H共线，即EH、BO、GF三线共点。
记BOG=，GOE=。连结EF交BO于K。只需证
=1（Ceva逆定理）。
=
=
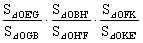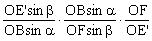=1
注：筝形：一条对角线垂直平分另一条对角线的四边形。
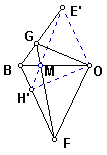对应于99联赛2：EOB=FOB，且EH、GF、BO三线共点。求证：GOB=HOB。
事实上，上述条件是充要条件，且M在OB延长线上时结论仍然成立。
证明方法为：同一法。
蝴蝶定理：P是⊙O的弦AB的中点，过P点引⊙O的两弦CD、EF，连结DE交AB于M，连结CF交AB于N。求证：MP=NP。
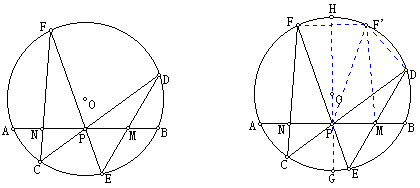
【分析】设GH为过P的直径，F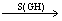
FF，显然⊙O。又PGH，PF=PF。∵PF
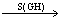PF，PA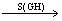
PB，FPN=FPM，PF=PF。
又FFGH，ANGH，FF∥AB。FPM+MDF=FPN+EDF
=EFF+EDF=180，P、M、D、F四点共圆。PFM=PDE=PFN。
△PFN≌△PFM，PN=PM。
【评注】一般结论为：已知半径为R的⊙O内一弦AB上的一点P，过P作两条相交弦CD、EF，连CF、ED交AB于M、N，已知OP=r，P到AB中点的距离为a，则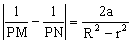
。（解析法证明：利用二次曲线系知识）
【竞赛专题讲座－平面几何四个重要定理】相关文章：
★ 高三数学强化训练
[标签：定理,几何,几何问题,讲座]
高考体育四项生的日常训练——深蹲移动跳：发展膝关节，踝关节力量。
张雪峰高考志愿填报指南 第28集 高考志愿分析，材料科学与工程专业，就业很一般，建议慎重选择
爆笑班主任 第一季 第220集 高考前最后一只视频，山东王老师揭秘高考的秘密
衍声高考琴行2019高本硕学生暑假音乐会 张俊瀚《陕北民歌主题变奏曲》《阿根廷舞曲》第三乐章
他高考作文仅得6分，总分428分，被985高校录取，却被导师拒绝！
