来自:查字典高考网 2009-08-31
一个半径为1的单位圆显然是可以盖住一个半径为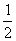 的圆的.反过来则不然,一个半径为
的圆的.反过来则不然,一个半径为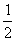 的圆无法盖住单位圆.那么两个半径为
的圆无法盖住单位圆.那么两个半径为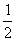 的圆能否盖住呢?不妨动手实验一下,不行.为什么不行?需几个这样的小圆方能盖住大圆?,这里我们讨论的就是覆盖问题,它是我们经常遇到的一类有趣而又困难的问题.
的圆能否盖住呢?不妨动手实验一下,不行.为什么不行?需几个这样的小圆方能盖住大圆?,这里我们讨论的就是覆盖问题,它是我们经常遇到的一类有趣而又困难的问题.
定义 设G和F是两个平面图形.如果图形F或由图形F经过有限次的平移、旋转、对称等变换扣得到的大小形状不变的图形F上的每一点都在图形G上.我们就说图形G覆盖图形F;反之,如果图形F或F上至少存在一点不在G上,我们就说图形G不能覆盖图形F.
关于图形覆盖,下述性质是十分明显的:
(1) 图形G覆盖自身;
(2) 图形G覆盖图形E,图形E覆盖图形F,则图形G覆盖图形F.
1.最简单情形――用一个圆覆盖一个图形.
首先根据覆盖和圆的定义及性质即可得到:
定理1 如果能在图形F所在平面上找到一点O,使得图形F中的每一点与O的距离都不大于定长r,则F可被一半径为r的圆所覆盖.
定理2 对于二定点A、B及定角若图形F中的每点都在AB同侧,且对A、B视角不小于,则图形F被以AB为弦,对AB视角等于的弓形G所覆盖.
在用圆去覆盖图形的有关问题的研究中,上述二定理应用十分广泛.
例1 求证:(1)周长为2l的平行四边形能够被半径为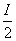 的圆面所覆盖.
的圆面所覆盖.
(2)桌面上放有一丝线做成的线圈,它的周长是2l,不管线圈形状如何,都可以被个半径为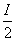 的圆纸片所覆盖.
的圆纸片所覆盖.
分析 (1)关键在于圆心位置,考虑到平行四边形是中心对称图形,可让覆盖圆圆心与平行四边形对角线交点叠合.
(2)"曲"化"直".对比(1),应取均分线圈的二点连线段中点作为覆盖圆圆心.
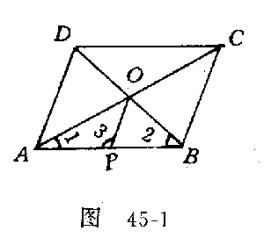
证明 (1)如图45-1,设ABCD的周长为2l,BDAC,AC、BD交于O,P为周界上任意一点,不妨设在AB上,则
3,
有OPOA.
又AC<AB+BC=l,
故OA<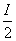 .
.
因此周长为2l的平行四边形ABCD可被以O为圆心;半径为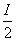 的圆所覆盖,命题得证.
的圆所覆盖,命题得证.
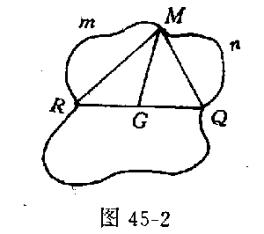
(2)如图45-2,在线圈上分别取点R,Q,使R、Q将线圈分成等长两段,每段各长l.又设RQ中点为G,M为线圈耻任意一点,连MR、MQ,则
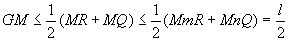
因此,以G为圆心,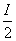 长为半径的圆纸片可以覆盖住整个线圈.
长为半径的圆纸片可以覆盖住整个线圈.
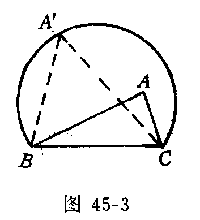
例2△ABC的最大边长是a,则这个三角形可被一半径为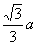 的圆所覆盖.
的圆所覆盖.
分析 a为最大边,所对角A满足60A<180.
证明 不妨设BC=a,以BC为弦,在A点所在一侧作含60角的弓形弧(图45-3).因60A,故根据定理2,△ABC可被该弓形所覆盖.
由正弦定理,弓形相应半径r=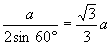 ,所以△ABC可被半径为
,所以△ABC可被半径为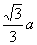 的圆所覆
的圆所覆
盖.
显然覆盖△ABC的圆有无穷多个,那么半径为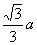 的圆是否是最小的覆盖圆呢?事实并不
的圆是否是最小的覆盖圆呢?事实并不
尽然.
例3 △ABC的最大边BC等于a,试求出覆盖△ABC的最小圆.
解 分三种情形进行讨论:
(1) A为钝角,以BC为直径作圆即可覆盖△ABC.
(2) A是直角,同样以BC为直径作圆即可覆盖△ABC;
(3)A是锐角.假若⊙O覆盖△ABC,我们可在⊙O内平移△ABC,使一个顶点B落到圆周上,再经过适当旋转,使另一个顶点落在圆周上,此时第三个顶点A在⊙O内或其圆周上,设BC所对圆周角为,那么,设⊙O直径d,△ABC外接圆直径d0,那么
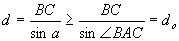
所以对于锐角三角形ABC,最小覆盖圆是它的外接圆.
今后我们称覆盖图形F的圆中最小的一个为F的最小覆盖圆.最小覆盖圆的半径叫做图形F的覆盖半径.
综合例2、例3,即知△ABC中,若a为最大边,则△ABC的覆盖半径r满足
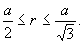
2.一个图形F能否被覆盖,与图形中任意两点间的距离最大值d密切相关.
以下我们称图形F中任意两点间的距离最大值d为图形F的直径.
我们继续研究多个圆覆盖一个图形问题.
定义 对于图形G1,G2,,Gn,若图形F中的每一点都被这组图形中的某个所覆盖,则称这几个图形覆盖图形F.
图形G1,G2,,Gn为n个圆是一特殊情形.
例4 以ABCD的边为直径向平行四边形内作四个半圆,证明这四个半圆一定覆盖整个平行四边形.
分析1 ABCD的每一点至少被某个半圆所盖住.
证明1 用反证法.如图45-4设存在一点P在以AB、BC、CD、DA为直径的圆外,根据定理二,APB,BPC,CPDDPA均小于90,从而
APB+BPC+CPD+DPA<360.
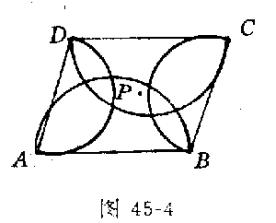
与四角和应为周角相矛盾.故P应被其中一半圆盖住,即所作四个半圆覆盖ABCD.
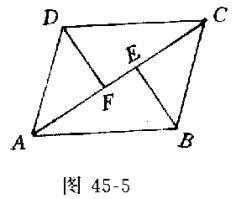
分析2 划片包干,如图45-5,将ABCD分为若干部分,使每一部分分别都被上述四个半圆所覆盖.
证明2 在ABCD中,如图45-5,设ACBD.分别过B、D引垂线BE、DF垂直AC,交AC于E、F,将ABCD分成四个直角三角形,△ABE、△BCE、△CDF、△DAF.每一个直角三角形恰好被一半圆所覆盖,从而整个四边形被四个半圆所覆盖.
上述结论可推广到任意四边形,留给读者考虑.
例5 求证:一个直径为1的圆不能被两个直径小于1的圆所覆盖.
证明 如图45-6,先考虑其中一个小圆即⊙O1去覆盖大圆O,连O1、O过O作ABO1O,AB为⊙O的直径(若O1、O重合,那么AB为任意直径)此时
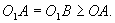
故A、B两点都不能被⊙O1盖住.至于另一小圆⊙O2无疑不能同时盖住A、B两点,故⊙O1、⊙O2不能覆盖⊙O.
事实上,我们还可以从另一角度给予证明.那就是一个小圆无法覆盖半个大圆,因此两个小圆也就不可能覆盖住整个大圆了.
现在,我们着手研究本文一开始就提出的问题.
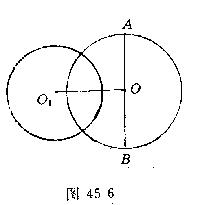
例6 给定一个半径为1的圆,若用半径为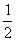 的圆去覆盖它,问至少要几个才能盖住.
的圆去覆盖它,问至少要几个才能盖住.
问题需要我们在二个方面给予回答:一是所确定数目的小圆足以覆盖大圆;二是少于确定的数目,则全部小圆不能覆盖大圆.
对于不能覆盖的推断,以下两个原则是常用的:
原则1 若图形F的面积大于图形G的面积,则图形G不能覆盖图形F.
原则2 直径为d的图形F不能被直径小于d的图形G所覆盖.
两原则十分显然,不再证明.
四个半径为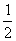 的小圆面积和为,恰等于大圆面积,而四小圆间若不重迭,则覆盖其它图形时,还须排除中间所夹的不属于四圆的部分,换句话说,四小圆所覆盖大圆部分面积必小于大圆自身面积,根据法则1,不可能覆盖大圆,少于四个小圆更不可能.
的小圆面积和为,恰等于大圆面积,而四小圆间若不重迭,则覆盖其它图形时,还须排除中间所夹的不属于四圆的部分,换句话说,四小圆所覆盖大圆部分面积必小于大圆自身面积,根据法则1,不可能覆盖大圆,少于四个小圆更不可能.
若有五个小圆,我们改变角度考虑,可将大圆周分为六等分.因小圆直径为1,五个小圆无法盖住大圆周,而六个圆周恰好盖住.
还需考虑大圆圆心没有被盖住,再添加一个小圆,符合要求!
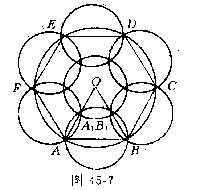
这说明:至少七个以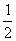 为半径的小圆方能覆覆盖半径为1的一个大圆.事实上这样的六个小圆若盖住大圆周,则大圆心不能被覆盖.若其中一小圆盖住大圆圆心,那么该圆又至多盖住大圆周上一点也就是六个小圆无法覆盖大圆,而我们作大圆的内接正六边形,分别将小圆圆心与各边中点重合,再将第七个小圆圆心与大圆圆心重合即可盖住大圆,如图45-7,以下给出证明:
为半径的小圆方能覆覆盖半径为1的一个大圆.事实上这样的六个小圆若盖住大圆周,则大圆心不能被覆盖.若其中一小圆盖住大圆圆心,那么该圆又至多盖住大圆周上一点也就是六个小圆无法覆盖大圆,而我们作大圆的内接正六边形,分别将小圆圆心与各边中点重合,再将第七个小圆圆心与大圆圆心重合即可盖住大圆,如图45-7,以下给出证明:
对于正△OAB,设OA、OB中点A1、B1,那么AA1B=AB1B=90,故四边形AA1B1B被以AB为直径的圆覆盖.另外,△OA1B1被小圆⊙O所覆盖.类似地可推得七个小圆覆盖整个大圆.
3.直线形图形覆盖别的图形的问题
解决直线形图形覆盖别的图形的问题,常须较高的智巧,一般的处理方法是通过构造过渡图形,逐步调整,最终获得问题的解决.
例7 证明直径为1的图形F可被单位正方形覆盖.
分析 先后用互相垂直的两对平行线将图形夹在中间,再向内收缩.
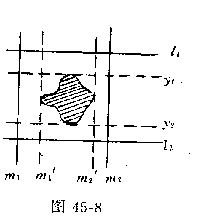
证明 取位于水平方向和铅直方向的两对平行直线将图形F夹在中间,再将位于下方的直线l2向上平移,直至遇到图形F上点为止,中图45-8中l2处.接着又将l1向下平移至与l2相距为1的l1处止.因图形F直径为1.故图形F仍被二直线l1,l2所夹.同样采用先左后右的顺序,将沿直线m1、m2平移至m1、m2处,m1、m2相距为1,而图形F依然夹在直线m1,m2中间,从而直线l1、l2、m1、m2所围成单位正方形即可覆盖图形F.
运用上述方法,我们可进一步解决以下问题:
例8 直径为1的图形F可被一个边长为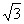 的正三角形覆盖,试证明之.
的正三角形覆盖,试证明之.
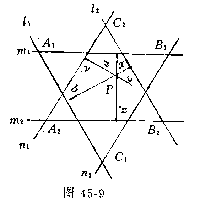
证明 作三对相距为1的平行直线m1、m2、n1、n2,l1、l2,相交直线所成角为60,围成可覆盖图形F的六边形及正△A1B1C1,正△A2B2C2(具体作法可参照例7).如图45-9.设P为F中任意一点,它到六边形各边距离依次为x、a、y、b、z、c.又设正△A1B1C1的高为h1,正△A2B2C2的高为h2.因正三角形内一点到三边距离和等于正三角形的高,得
a+b+c=h1,
x+y+z=h2.
相加,得
(x+b)+(y+c)+(z+a)=h1+h2,
又x+b=1,y+c=1,z+a=1,
h1+h2=3.
根据抽屉原则,h1、h2中有一不大于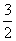 ,不妨设
,不妨设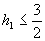 ,即正△A1B1C1的高不大于
,即正△A1B1C1的高不大于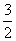 ,那么它的边长
,那么它的边长
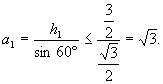
因此图形F可被边长不大于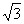 的正三角形即正△A1B1C1所覆盖.
的正三角形即正△A1B1C1所覆盖.
4.图形的嵌入是覆盖问题的一种重要变化形式
所谓图形F能嵌入图形G,其本质就是图形G能覆盖图形F.
例9试证面积为S、周长为P的四边形一定可嵌入一个半径为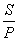 的圆.
的圆.
分析 四边形内存在到各边距离不小于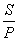 的点.
的点.
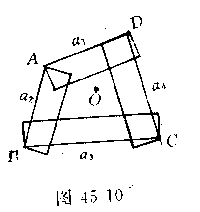
证明 如图45-10,设四边形ABCD面积为S,周长为P.各边长分别为a1、a2、a3、a4.现以a1、a2、a3、a4为长,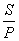 为宽,向四边形内侧作矩形,则这些矩形总面积是
为宽,向四边形内侧作矩形,则这些矩形总面积是
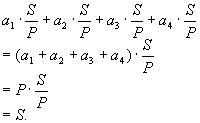
即四个矩形面积总和等于四边形面积.由于这四个矩形有重迭部分,所以四边形内部存在点O没有被矩形覆盖,那么以点O为圆心,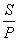 为半径的圆可嵌入四边形ABCD中.
为半径的圆可嵌入四边形ABCD中.
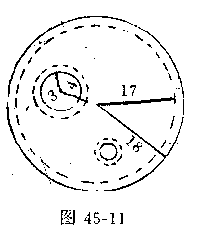
例10 在一个半径等于18的圆中已嵌入16个半径为3的圆.证明在余下的部分中还能嵌入9个半径为1的圆.
证明 首先证明大圆中还能嵌入1个半径为1的小圆.先将大圆的半径收缩为17,而将半径为3的圆膨胀成半径为4的圆,此时大圆面积变为
172=289.
16个半径为4的圆的面积是
4216=256.
289=33.
这说明大圆中嵌入16个半径为3的圆外,还能嵌入半径为1的一个小圆,如图45-11所示.
再将大圆的半径收缩为17,半径为3的圆的半径膨胀为4,半径为1的圆膨胀为2,由于
289-4,所以大圆中除嵌入16个半径为3的圆外,还能嵌入两个半径为1的圆.依此类推,由于289-48=>0,
故大圆还可嵌入九个半径为1的小圆.
将图形收缩、膨胀是解嵌入问题一种重要方法.
【覆盖】相关文章:
★ 2020年高校已开放2.4万门在线课 覆盖本科12个学科
[标签:图形]
张雪峰高考志愿填报指南 第15集 高考填报志愿,想学电子信息类专业,推荐报这六所高校,不出错
学渣儿子高考,英语选择题全选B!老师通报成绩的那一刻父亲懵了
广州早晨 2019 山西一高中班主任带学生骑行1800公里去上海
高考阅卷名师给考生的高考作文密训课 第4集 高考作文审题实操方法精讲(二)
1000张学生用草稿纸考研专用免邮空白便宜薄演草演算纸白纸本书写纸批发打草a4大张实惠装18k高考数学草稿本
amc传媒音乐影像 第一季 第600集 高中校长演唱《记忆花园》为高考学子助力打气
爆笑班主任 第一季 第220集 高考前最后一只视频,山东王老师揭秘高考的秘密
张雪峰高考志愿填报指南 第28集 高考志愿分析,材料科学与工程专业,就业很一般,建议慎重选择
衍声高考琴行2019高本硕学生暑假音乐会 张俊瀚《陕北民歌主题变奏曲》《阿根廷舞曲》第三乐章